Modelagem do Conversor Cúk

Este trabalho se propõe em realizar a obtenção dos modelos Chaveado, Médio Não Linear e Médio Linearizado do conversor CC-CC de topologia Cúk. Inicialmente são apresentadas as características gerais do conversor e seu circuito típico. Em seguida, as equações diferenciais que descrevem o circuito do conversor são obtidas para obter os modelos matemáticos do Cúk assim como a sua relação de transformação no modo de condução contínua. Por final realizou-se em Matlab/Simulink as simulações do conversor Cúk com os modelos desenvolvidos para uma variação degrau da relação cíclica e da tensão de entrada. A obtenção dos modelos considera somente o modo de condução contínua do conversor.

Características Gerais do Conversor Cúk.

Conversores CC-CC se baseiam no princípio de transferência de energia entre a entrada e saída através de um elemento reativo. O conversor com topologia Cúk utiliza-se de um capacitor para realizar a transferência de energia entre a fonte e carga [1]. Este conversor é dual do conversor redutor elevador tipo Buck-Boost e está esquematizado na Figura 1. As trocas de energia entre a entrada e a saída são feitas através do condensador C1 e a tensão de saída tem a polaridade invertida em relação à fonte tensão Vg. A grande vantagem deste conversor consiste no reduzido tremor das correntes de entrada e de saída. A redução das ondulações de corrente pode ser ainda maior, caso as indutâncias forem mutuamente acopladas [1].

O conversor de Cúk tem a vantagem de produzir um baixo ruído EMI por possuir baixo valor de ondulação nas correntes de entrada e saída. A desvantagem deste conversor está na utilização de um capacitor para a transferência de energia entre a entrada e a saída [1]. O processo de transferência de energia só é eficaz para potências não muito elevadas, pois caso contrário é necessário aumentar a capacitância C1 provocando uma redução do rendimento devido aumento das perdas no capacitor.

Figura 1 - Conversor CC tipo Cúk.

O conversor Cúk apresentado na Figura 1 funciona em duas situações distintas que são definidas pelo estado da chave semicondutora presente no circuito. O Cúk pode funcionar no modo de condução descontinuo que se caracteriza pela completa descarga do capacitor , no modo continuo a tensão no capacitor não se anula [2]. Em funcionamento em modo contínuo, o ganho de tensão depende apenas da relação cíclica, mas no funcionamento em modo descontínuo, o ganho depende da frequência de comutação e da resistência de carga. Os parâmetros do conversor são organizados na Tabela 1.

Funcionamento e Modelos do Conversor Cúk.

O circuito tem duas situações distintas definidas pelo estado da chave semicondutora. Assumindo que o converso opere no modo de condução contínuo, podem-se considerar os dois circuitos apresentados nas Figura 2 e Figura 3 para a chave fechada e aberta respectivamente.
Quando a chave do circuito está fechada a fonte Vg armazena energia na indutância L1 e o capacitor C1 com tensão V1 transfere sua energia através da indutância L2 para suprir a carga, neste instante o diodo D1 não conduz, pois ele se encontra reversamente polarizado pela tensão V1 do capacitor C1.

Figura 2 - Circuito Cúk com Chave Fechada

No momento que a chave é aberta o diodo D1 se polariza diretamente e passa a conduzir a corrente IL1 que carrega o capacitor com uma tensão superior a da fonte de entrada. A carga passa a ser suprida pela energia armazenada na indutância L2.

Figura 3 - Circuito Cúk com Chave Aberta.

Equações Diferenciais do Conversor Cúk.

Considerando o funcionamento do circuito podem-se deduzir quatro equações para cada estado da chave semicondutora. As equações e as matrizes de espaço de estados, presente na Tabela 2, são referentes a chave fechada e aberta do circuito das Figura 2 e 3, respectivamente.

Modelo Chaveado do Conversor Cúk.

O modelo chaveado do conversor é obtido intercalando os dois sistemas de equações através da
função d(t), como mostrado em (1). Ou de forma mais compacta, pode-se definir (3).

Modelo médio não Linear do Conversor Cúk.

As equações do sistema em sua forma bilinear é apresentado em (5). O valor médio dessa equação, que não é linear, define o modelo médio não linear do sistema. Portando, para uma dada entrada de sinal médio têm-se as saída médias do sistema.

Modelo médio Linearizado

Pode-se observa pelas equações (3) que o conversor não é linear. A presença dos produtos entre termos dependente do tempo fornecem um sistema não linear. Um modelo linear para pequenos sinais se torna desejável em projetos de controladores clássicos. A equação (3) admite uma linearização entorno de um ponto médio de operação onde as variações em torno desse ponto são pequenas.

Para um determinado ponto de funcionamento do Cúk  pode-se aproximar os estados do sistema
da forma  [x(t)]=[X]+[x ̃(t)] como definido em (6).

Aplicando a aproximação definida em (6), obtém-se a equação matricial (7).

Com algumas manipulações algébricas é possível redefinir a equação (7) na forma de (8). Com essa nova equação observam-se duas componentes lineares, sendo uma CC e outra AC de 1° ordem e uma terceira componente AC não linear. Onde A e B são as matrizes ponderadas definidas em (9).

A componente de segunda ordem é desconsiderada no modelo linearizado, pois sua influência para pequenos sinais se torna pequena sendo aproximada como um ruído do modelo. Assim o modelo linearizado do conversor é definido pela equação (10).

Relação de Transformação do Conversor Cúk

A relação de transformação do conversor é obtida para o modo de condução contínua. Em regime permanente as oscilações em torno do ponto médio são pequenas podendo ser desconsideradas (11), assim os estados do sistema podem ser definidos pelas componentes contínua do modelo. Portanto para uma dada relação cíclica e tensão de entrada obtemos (12).

Resolvendo (12) para Vo encontra-se a relação de transformação do conversor Cúk com perdas. Na Tabela 3 compra a relação de transformação para um caso ideal e com perdas nas indutâncias.

A Figura 4 apresenta o ganho da tensão de saída em função da relação cíclica para o conversor Cúk estudado considerando um caso com perdas e sem perdas. O ganho máximo do conversor com os parâmetros especificados da Tabela 1 é de −1,98 para uma relação cíclica D=0,82 .

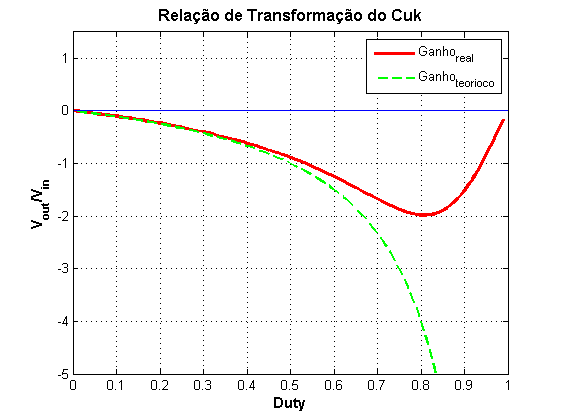Figura 4 - Ganho de tensão do conversor Cúk ideal e com perdas.

Resultados Simulados dos Modelos do Conversor Cúk. 

Foi desenvolvido em Matlab/Simulink a simulação do conversor Cúk para os modelos chaveados, médio não linear e médio linearizado. As respostas apresentadas das variáveis de estados para os três modelos correspondem, num primeiro momento ao funcionamento em regime permanente (Figuras 6 e 7), em seguida para uma variação da razão cíclica de chaveamento (Figuras de 8 à 11) e por final são apresentadas as variáveis de estados do conversor em função a uma perturbação da tensão de entrada (Figuras 12 à 15). Os modelos simulados são ilustrados de forma esquemática na Figura 5.

Figura 5 - Esquemático da Simulação  dos modelos desenvolvidos.

Inicialmente considerou-se a tensão de entrada constante em Vg=10V para os três modelos e uma razão cíclica de D=0,3501 com o objetivo de se obter uma tensão de saída de 5V. As Figura 6 e Figura 7 apresentam os estados do conversor nos três modelos. O modelo Chaveado é representado em vermelho e os modelos Médio não Linear e Médio Linearizado são expostos na cor verde e azul respectivamente. Vale notar que o modelo chaveado possui ondulações em seus estados, pois o modelo considera os efeitos de chaveamento do circuito, já os outros dois modelos esse efeito não é considerado pois suas entradas estão em função dos seus valores médios. 

Figura 6 - Tensão de saída Vo e Tensão sobre o capacitor C1  Vc1.

Figura 7 - Corrente de entrada (IL1) e corrente sobre o Indutor L2 (IL2)

Em  seguida  variou-se  a  relação  cíclica  do  conversor  de D=0,3501 para D=0,4501 em t=6ms.  As
Figura  8,  Figura  9,  Figura  10  e  Figura  11  apresentam  o  comportamento  dos  quatros  estados  do
sistema Cúk para os modelos Chaveados, Médio Não Linear e Médio Linearizado respectivamente.

Na  situação  de  variação  da  relação  cíclica  o  modelo  médio  linearizado  apresenta  um  erro considerável em amplitude, pois a linearização não  contempla  outros pontos de funcionamento do sistema o que limita o modelo para pequenas variações próximas do ponto quiescente projetado.

Em um segundo momento manteve-se a relação cíclica do conversor constante em D=0,3501 e variou-se, em forma de degrau, a tensão de entrada (Vg) do conversor de 10V para 12V. Nas Figura 12, Figura  13,  Figura  14  e Figura  15  apresentam o comportamento dos quatros estados do conversor Cúk para os modelos Chaveado, Médio Não Linear e Médio Linearizado respectivamente.

É possível observar pelos gráficos das figuras acima que o modelo médio linearizado e médio não linear possuem o mesmo comportamento e correspondem ao valor médio do modelo chaveado. De fato esse comportamento do modelo linearizado é previsto pela equação (8), pois a componente CA  da  relação  cíclica  é  zero  quando d(t) é constante,  logo  a  equação  (8)  nessa  situação  é equivalente a equação (5) do modelo médio não linear.

Conclusão

Os  modelos  desenvolvidos  tendem  a  representar  o  sistema  real  através  de  simplificações  e considerações  de  funcionamento.  O  modelo  chaveado  se  aproxima  de  forma  mais  completa  da operação  do  conversor,  pois  o  processo  de  chaveamento  é  considerado  no  modelo,  entretanto  a modelagem  chaveada  não  considerou  todos  os  elementos  parasitas  do  circuito  como  perdas  nos dispositivos  semicondutores  e  capacitores.  O  modelo  não  linear  descreve  o  comportamento  do conversor  sem  a  influência  do  chaveamento  e  é  útil  para  obter  o  valor  médio  das  trajetórias  dos estados  do  sistema.  O  modelo  linearizado  representa  o  sistema  para  um  determinado  ponto  de operação  sendo  limitado  para  outras  condições  de  trabalho porem essa técnica de modelagem por linearização se torna útil  para o projeto de controladores clássicos (PI e PID).

Referências

1. MANUEL , J. D. C. Apontamentos de Eletrónica de Potência II. [S.l.]. 2000.
2. ERIKSON, R. W. Fundaments of Power Electronics. [S.l.]: Ed. Chapman & Hall, 1997.

3. SELEME I. S. Modelagem e Controle de Conversores Estáticos.